Uno de los mayores retos matemáticos con los que se enfrentan los métodos de simulación numérica, es la resolución de las ecuaciones diferenciales en derivadas parciales, que plantea la resolución de la ecuación de Schrodinger; su resolución ,aplicada a los sistemas moleculares compuestos de muchos cuerpos, es necesaria para describir los sistemas cuánticos, su estructura electrónica, la dinámica de las partículas subatómicas y sus propiedades físicas y químicas.
Con frecuencia en estos casos, es necesario resolver la ecuación de Schrodinger, dentro de un espacio de múltiples dimensiones espaciales, que los métodos numéricos no pueden resolver utilizando, incluso, los superordenadores de última generación.
La resolución de La Ecuación Molecular no Relativista Independiente del Tiempo de Schrodinger (EMNRINT):

(7), solo es posible para moléculas muy simples; esto es debido a que el esfuerzo de cálculo necesario crece de modo exponencial con el incremento del número de electrones de un sistema; la dificultad creciente para realizar los cálculos está causada por la repulsión electrónica, llegando a ser pronto impracticable el cálculo.
La función :

es una auto función de onda de de muchos electrones, que contiene el conjunto de números cuánticos correspondientes, con todos los grados de libertad (coordenadas) de todos los electrones y núcleos de un sistema molecular;

es una función que depende de las coordenadas de los núcleos

y es el autovalor de la energía del Hamiltoniano completo H, al ser añadido el término

(8) y (9) correspondientes, respectivamente, al operador de la energía cinética de los núcleos y al operador de la energía potencial de la interacción de repulsión de Coulomb entre los núcleos.
Bibliografía:
- [1]
- [2]
- [3]
- [4]
La ecuación (7) solo puede ser resuelta de modo exacto, para átomos o moléculas muy simples (ej. la molécula H2).
Es, por tanto, un objetivo primordial tener la posibilidad de resolver, de modo aproximado mediante simulación numérica, la ecuación (EMNRINT); esto solo sería posible, utilizando el enorme potencial de una incipiente tecnología de la computación cuántica, cuando ésta sea eficiente.
La utilización de la mecánica cuántica es necesaria para describir y determinar, de modo aproximado, las estructuras electrónicas atómicas y moleculares, para mejorar el conocimiento de la naturaleza de los enlaces químicos entre los átomos, las moléculas y los grupos de moléculas y poder conocer sus propiedades.

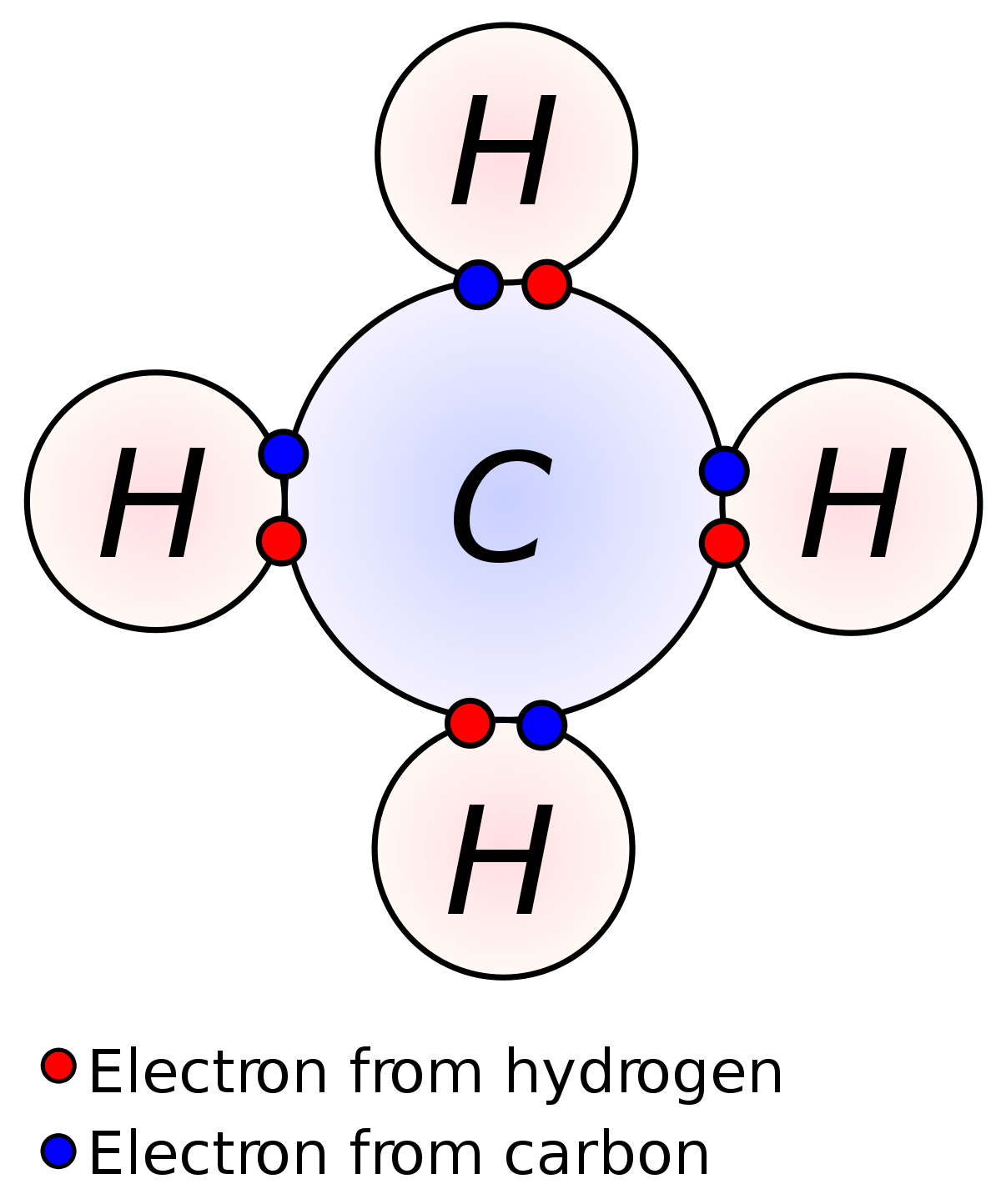
Figura 3:
molécula de metano CH4 (enlace covalente);

Figura 4:
Estructura de la molécula de agua (Martin Chaplin 2018)
Las moléculas pueden ser consideradas como un conjunto de (N) núcleos y de (n) electrones sometidos a las leyes de la mecánica cuántica; su formación se realiza mediante diversos tipos de enlaces o uniones de átomos.
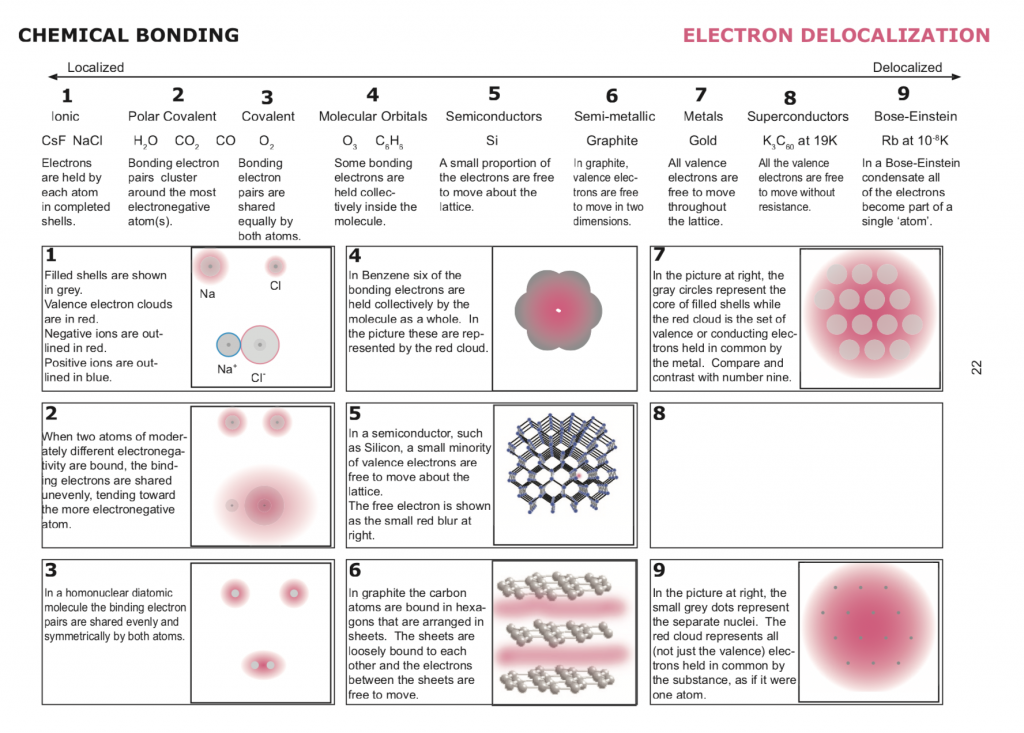
Tipos de enlaces químicos (Stephen Thomson/Joe Staley)
La computación numérica tradicional está limitada a sistemas poco complejos de tamaño pequeño; cuando se necesita un nivel de precisión elevado, la computación numérica tradicional se hace ineficiente y en muchos casos inabordable.
Las limitaciones que presenta la computación clásica, pueden ser superadas con la incipiente Computación Cuántica.